because it is accustomed to 'project' all light impressions rectilinearly out into space (Fig. 12b.). Hence, it sees P in the position of P'. This is thought to be the origin of the impression that the whole bottom of the vessel is raised.

This kind of explanation is quite in line with the peculiarity of the onlooker-consciousness, noted earlier, to attribute an optical illusion to the eye's way of working, while charging the mind with the task of clearing up the illusion. In reality it is just the reverse. Since the intellect can form no other idea of the act of seeing than that this is a passive process taking place solely within the eye, it falls, itself, into illusion. How great is this illusion we see from the fact that the intellect is finally obliged to make the eye somehow or other 'project' into space the impressions it receives - a process lacking any concrete dynamic content.

Once more, it is not our task to replace this way of 'explaining' the phenomenon by any other, but rather to combine the phenomenon given here with others of kindred nature so that the theory contained in them can be read from them direct. One other such phenomenon is that of so-called apparent optical depth, which an observer encounters when looking through transparent media of varying optical density. What connects the two is the fact that the rate of the alteration of depth, and the rate of change of the direction of light, are the same for the same media.

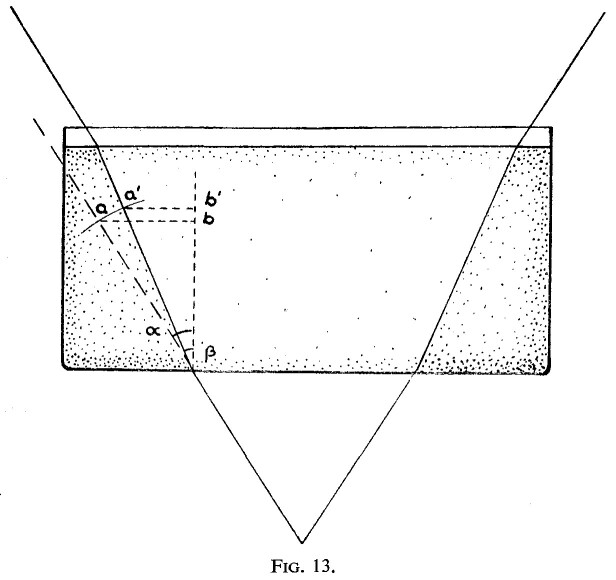
In present-day optics this phenomenon is explained with reference to the former. In proceeding like this, optical science makes the very mistake which Goethe condemned in Newton, saying that a complicated phenomenon was made the basis, and the simpler derived from the complex. For of these two phenomena, the simpler, since it is independent of any secondary condition, is the one showing that our experience of depth is dependent on the density of the optical medium. The latter phenomenon we met once before, though without reference to its quantitative side, when in looking at a landscape we found how our experiences of depth change in conformity with alterations in atmospheric conditions. This, then, served to make us aware that the way we apprehend things optically is the result of an interplay between our visual ray and the medium outside us which it meets.

It is exactly the same when we look through a vessel filled with water and see the bottom of it as if raised in level. This is in no sense an optical illusion; it is the result of what takes place objectively and dynamically within the medium, when our eye-ray passes through it. Only our intellect is under an illusion when, in the case of the coin becoming visible at the bottom of the vessel, it deals with the coin as if it were a point from which an individual ray of light went out.. .. etc., instead of conceiving the phenomenon of the raising of the vessel's bottom as one indivisible whole, wherein the coin serves only to link our attention to it.

Having thus cleared away the kinematic interpretation of the coin-in-the-bowl phenomenon, we may pass on to discuss the optical effect through which the so-called law of refraction was first established in science. Instead of picturing to ourselves, as is usually done, light-rays which are shifted away from or towards the perpendicular at the border-plane between two media of different optical properties, we shall rather build up the picture as light itself designs it into space.

We have seen that our inner light, as well as the outer light, suffers a certain hindrance in passing through a physical medium - even such as the earth's gravity-field. Whilst we may not describe this retardation, as is usually done, in terms of a smaller velocity of light itself within the denser medium, we may rightly say that density has the effect of lessening the intensity of the light. (It is the time required for the initial establishment of a light-filled realm which is greater within such a medium than outside it.) Now by its very nature the intensity of light cannot be measured in spatial terms. Yet there is a phenomenon by which the decrease of the inner intensity of the light becomes spatially apparent and thus spatially measurable. It consists in the alteration undergone by the aperture of a cone of light when passing from one optical medium to another.

If one sets in the path of a luminous cone a glass-walled trough filled with water, then, if both water and surrounding air are slightly clouded, the cone is seen to make a more acute angle within the water than outside it (Fig. 13). Here in an external phenomenon we meet the same weakening in the light's tendency to expand that we recognized in the shortening of our experience of depth on looking through a dense medium. Obviously, we expect the externally observable narrowing of the light-cone and the subjectively experienced change of optical depth to show the same ratio.

In order to compare the rate of expansion of a luminous cone inside and outside water, we must measure by how much less the width of the cone increases within the water than it does outside. (To be comparable, the measurements must be based upon the same distances on the edge of the cone, because this is the length of the way the light actually travels.) In Fig. 13 this is shown by the two distances, a-b and a'-b'. Their ratio is the same as that by which the bottom of a vessel appears to be raised when the vessel is filled with water (4:3).