c12p23

*

c12p39

c12p8

For the purpose of this book it is not necessary to expound in detail why modern mathematical thinking has been led to look for thought-forms other than those of classical geometry. It is enough to remark that for quite a long time there had been an awareness of the fact that the consistency of Euclid’s definitions and proofs fails as soon as one has no longer to do with finite geometrical entities, but with figures which extend into infinity, as for instance when the properties of parallel straight lines come into question. For the concept of infinity was foreign to classical geometrical thinking. Problems of the kind which had defeated Euclidean thinking became soluble directly human thinking was able to handle the concept of infinity.

c12p24

When we set out earlier in this book (Chapter VIII) to discover the source of Galileo’s intuition, by which he had been enabled to find the theorem of the parallelogram of forces, we were led to certain experiences through which all men go in early childhood by erecting their body and learning to walk. We were thereby led to realize that man’s general capacity for thinking mathematically is the outcome of early experiences of this kind. It is evident that geometrical concepts arising in man’s mind in this way must be those of Euclidean geometry. For they are acquired by the will’s struggle with gravity. The dynamic law discovered in this way by Galileo was therefore bound to apply to the behaviour of mechanical forces – that is, of forces acting from points outward.

c12p40

the point diminishing gradually. Since we remain all the time on the surface, we have no reason to conceive any change in its original position; that is, we continue to think of it as an all-embracing plane with regard to the chosen point.

c12p9

We shall now indicate some of the lines of geometrical thought which follow from this.

c12p7

Einstein owed the possibility of establishing his space-picture to a certain achievement of mathematical thinking in modern times. As we have seen, one of the peculiarities of the onlooker-consciousness consists in its being devoid of all connexion with reality. The process of thinking thereby gained a degree of freedom which did not exist in former ages. In consequence, mathematicians were enabled in the course of the nineteenth century to conceive the most varied space-systems which were all mathematically consistent and yet lacked all relation to external existence. A considerable number of space-systems have thus become established among which there is the system that served Einstein to derive his space-time concept. Some of them have been more or less fully worked out, while in certain instances all that has been done is to show that they are mathematically conceivable. Among these there is one which in all its characteristics is polarically opposite to the Euclidean system, and which is destined for this reason to become the space-system of levity. It is symptomatic of the remoteness from reality of mathematical thinking in the onlooker-age that precisely this system has so far received no special attention.¹

c12p25

In a similar way we can now seek to find the source of our capacity to form polar-Euclidean concepts. As we were formerly led to experiences of man’s early life on earth, so we are now led to his embryonic and even pre-embryonic existence.

c12p41

The only way of representing the sphere diagrammatically, as a unit bearing in itself the character of the plane whence it sprang, is as shown in Fig. 9, where a number of planes, functioning as tangential planes, are so related that together they form a surface which possesses everywhere the same distance from the all-relating point.

c12p10

Let us consider a straight line extending without limits in either direction. Projective geometry is able to state that a point moving along this line in one direction will eventually return from the other. To see this, we imagine two straight lines a and b intersecting at P. One of these lines is fixed (a); the other (b) rotates uniformly about C. Fig. 7 indicates the rotation of b by showing it in a number of

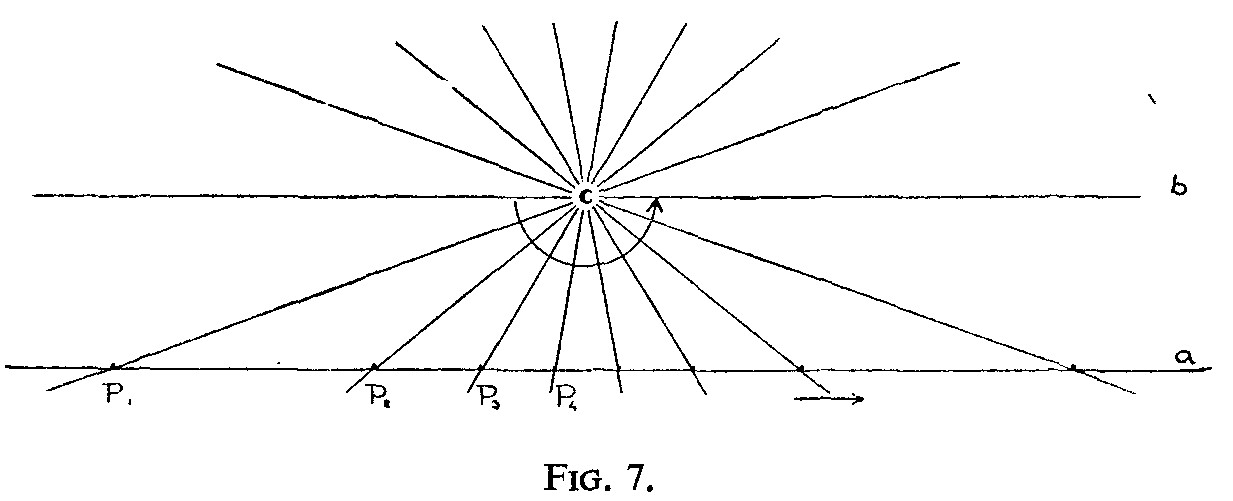
positions with the respective positions of its point of intersection with a (P₁, P₂. . .). We observe this point moving along a, as a result of the rotation of b, until, when both lines are parallel, it reaches infinity. As a result of the continued rotation of b, however, P does not remain in infinity, but returns along a from the other side. We find here two forms of movement linked together – the rotational movement of a line (b) on a point (C), and the progressive movement of a point (P) along a line (a). The first movement is continuous, and observable throughout within finite space. Therefore the second movement must be continuous as well, even though it partly escapes our observation. Hence, when P disappears into infinity on one side of our own point of observation, it is at the same time in infinity on the other side. In order words, an unlimited straight line has only one point at infinity.