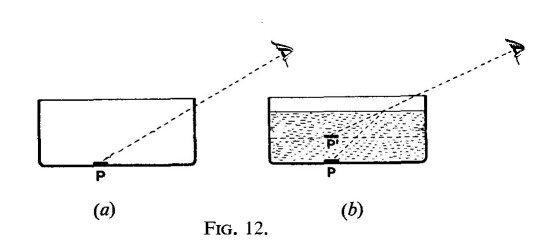
c17p41

consists in the fact, surprising at first sight, that an object, such as a coin, which lies at the bottom of a vessel hidden from an observer by the rim, becomes visible when the vessel is filled with water. Modern optics has explained this by assuming that from the separate points of the floor of the vessel light-rays go out to all sides, one ray falling in the direction of the eye of the observer. Hence, because of the positions of eye and intercepting rim there are a number of points from which no rays can reach the eye. One such point is represented by the coin (P in Fig. 12a). Now if the vessel is filled with water, light-rays emerging from it are held to be refracted, so that rays from the points hitherto invisible also meet the eye, which is still in its original position. The eye itself is not conscious of this ‘break’ in the light-rays,

c17p57

¹ Compare with this our account in Chapter X of the rise of the atomistic-kinematic interpretation of heat.

c17p10

With the last assertion we do not mean to say that there is nothing going on in connexion with the appearance of optical phenomena to which the concept of a finite velocity is applicable. Only, what is propagated in this way is not the entity we comprise under the concept of ‘light’. Our next task, therefore, will be to create a proper distinction between what moves and what does not move spatially when light is active in the physical world. Once more an historical retrospect will help us to establish our own standpoint with regard to the existing theories.

c17p26

Precisely the same criticism applies to Bradley’s observation, and to an even higher degree. What Bradley discovered is the fact that the apparent direction in which we see a fixed star is dependent on the direction in which the earth moves relatively to the star, a phenomenon known under the name of ‘aberration of light’. This phenomenon is frequently brought to students’ understanding by means of the following or some similar analogy.

c17p42

c17p58

² The following critical study leaves, of course, completely untouched our recognition of the devotion which guided the respective observers in their work, and of the ingenuity with which some of their observations were devised and carried out.

c17p11

The first to think of light as possessing a finite velocity was Galileo, who also made the first, though unsuccessful, attempt to measure it. Equally unsuccessful were attempts of a similar nature made soon afterwards by members of the Accademia del Cimento. In both cases the obvious procedure was to produce regular flashes of light and to try to measure the time which elapsed between their production and their observation by some more or less distant observer. Still, the conviction of the existence of such a velocity was so deeply ingrained in the minds of men that, when later observations succeeded in establishing a finite magnitude for what seemed to be the rate of the light’s movement through space, these observations were hailed much more as the quantitative value of this movement than as proof of its existence, which was already taken for granted.

c17p27

Imagine that a machine-gun in a fixed position has sent its projectile right across a railway-carriage so that both the latter’s walls are pierced. If the train is at rest, the position of the gun could be determined by sighting through the shot-holes made by the entrance and exit of the bullet. If, however, the train is moving at high speed, it will have advanced a certain distance during the time taken by the projectile to cross the carriage, and the point of exit will be nearer the rear of the carriage than in the previous case. Let us now think of an observer in the train who, while ignorant of the train’s movement, undertook to determine the gun’s position by considering the direction of the line connecting the two holes. He would necessarily locate the gun in a position which, compared with its true position, would seem to have shifted by some distance in the direction of the train’s motion. On the other hand, given the speed of the train, the angle which the line connecting the two holes forms with the true direction of the course of the projectile – the so-called angle of aberration – provides a measure of the speed of the projectile.

c17p43

because it is accustomed to ‘project’ all light impressions rectilinearly out into space (Fig. 12b.). Hence, it sees P in the position of P’. This is thought to be the origin of the impression that the whole bottom of the vessel is raised.

c17p59

³ The assumption is that the wave-velocity differs from the group-velocity, if at all, by a negligible amount.