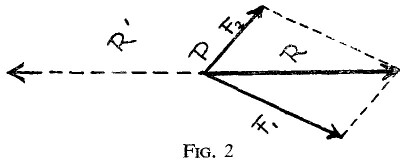
c8p58

Having in this way removed the fallacious idea that the parallelogram of forces can, and therefore ever has been, conceived by way of logical derivation from the parallelogram of velocities, we must then ask ourselves what it was, if not any act of logical reason, that led Galileo to discover it.

c8p11

To begin with, the well-known fact is cited that if one plunges one’s hands first into two different bowls, one filled with hot water and the other with cold, and then plunges them together into a bowl of tepid water, this will feel cold to the hand coming from the hot water and warm to the hand coming from the cold. Next, it is pointed out that two thermometers which are put through the same procedure will register an equal degree of temperature for the tepid water. In this way the student is given a lasting impression of the superiority of the ‘objective’ recording of the instrument over the ‘subjective’ character of the experiences mediated by his sense of warmth.

c8p27

c8p43

To find an interpretation of the formula F=ma, which is free from illusion, we must turn our attention first of all to the concepts ‘force’ and ‘mass’ themselves. The fact that men have these two words in their languages shows that the concepts expressed by them must be based on some experience that has been man’s long before he was capable of any scientific reflexion. Let us ask what kind of experience this is and by what part of his being he gathers it.

c8p59

History relates that on making the discovery he exclaimed: ‘La natura è scritta in lingua matematica!‘ (‘Nature is recorded in the language of mathematics.’) These words reveal his surprise when he realized the implication of his discovery. Still, intuitively he must have known that using geometrical lengths to symbolize the measured magnitudes of forces would yield some valid result. Whence came this intuition, as well as the other which led him to recognize from the figures thus obtained that in a parallelogram made up of any two of the three lines, the remaining line came in as its diagonal? And, quite apart from the particular event of the discovery, how can we account for the very fact that nature – at least on a certain level of her existence – exhibits rules of action expressible in terms of logical principles immanent in the human mind?

c8p12

Let us now test this procedure by carrying out the same experiment with the help of thermometrical instruments in their original form, that is, the form in which Galileo first applied them. By doing so we proceed in a truly Goethean manner, because we divest the experiment of all accessories which prevent the phenomenon from appearing in its primary form.

c8p28

c8p44

The answer is, as simple self-observation will show, that we know of the existence of force through the fact that we ourselves must exert it in order to move our own body. Thus it is the resistance of our body against any alteration of its state of motion, as a result of its being composed of inert matter, which gives us the experience of force both as a possession of our own and as a property of the outer world. All other references to force, in places where it cannot be immediately experienced, arise by way of analogy based on the similarity of the content of our observation to that which springs from the exertion of force in our own bodies.

c8p60

To find the answer to these questions we must revert to certain facts connected with man’s psycho-physical make-up of which the considerations of Chapter II have already made us aware.

c8p13

To turn a modern thermometer into a thermoscope we need only remove the figures from its scale. If we make the experiment with two such thermoscopes we at once become aware of something which usually escapes us, our attention being fixed on the figures recorded by the two instruments. For we now notice that the two instruments, when transferred from the hot and cold water into the tepid water, behave quite differently. In one the column will fall, in the other it will rise.